优美树验证项目
优美树验证项目(Graceful Tree Verification Project,简称GTV)是由 fwjmath 个人建立的数学类分布式计算项目.本项目旨在通过志愿分布式计算的方式对优美树猜想进行验证。优美树猜想是图论中一个重要但悬而未决的猜想,它猜想所有的树都是优美的。通过这个项目的计算,我们可以对优美树猜想进行验证,试图寻找反例,同时获得优美树的一些统计性质,帮助数学家更好的研究优美树猜想。
如何加入项目
该项目基于 BOINC 平台,简要的加入步骤如下(已完成的步骤可直接跳过):
- 下载并安装 BOINC 的客户端软件(官方下载页面或程序下载)
- 点击客户端简易视图下的“Add Project”按钮,或高级视图下菜单中的“工具->加入项目”,将显示向导对话框
- 点击下一步后在项目列表中找到并单击选中 Yoyo@home 项目(如未显示该项目,则在编辑框中输入项目网址:http://www.rechenkraft.net/yoyo/ ),然后点击下一步
- 输入您可用的电子邮件地址,并设置您在该项目的登录密码(并非您的电子邮件密码)
- 再次点击下一步,如项目服务器工作正常(并且有适合自身操作系统的计算程序),即已成功加入项目
更详细的加入方法说明,请访问 BOINC 新手指南 或 BOINC 使用教程。
本站推荐您加入 Team China 团队,请访问项目官方网站的 团队检索页面,搜索(Search)并进入 Team China 的团队页面,点击页面中的 Join 并输入用户登录信息即可加入!加入后,请选择Harmonious Trees子项目。
独立项目
优美树验证项目曾经以独立项目方式运行。项目目前已暂停,仅通过yoyo@home运行。计算结果及算法发表在预印本网站arxiv.org上(论文地址)。项目验证了,含有不超过 35 个顶点的树都是优美树。
项目数学背景
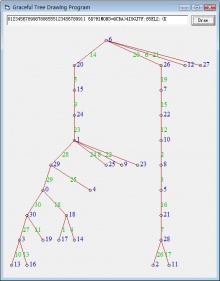
优美树的定义
如图所示,这是一棵有31个顶点的树,如果您数一数的话会发现这些顶点旁边被标记了从0到30的数字,没有两个不同的顶点标记了相同的数字,而每个数字都在这棵树上出现了。这叫一个标号。
如果我们看边上标记的数字的话,您会发现它们恰好是这条边的两个顶点的标记数字的差。这种边上的标记就叫由顶点标号诱导出来的一个边的标号。
这棵树一共有30条边。如果我们仔细数一数边上的数字的话,会发现从1到30的数字都碰巧出现了,满足这种条件的标号就叫做一个优美标号(graceful labelling)。
一般地说,一棵拥有n个顶点的树有n-1条边,如果存在一个对顶点进行从0到n-1的不重不漏的标号,它所诱导出来的边的标号恰好不重不漏为1到n-1的话,我们就把这个顶点的标号称为一个优美标号。
如果一棵树能拥有至少一个优美标号的话,我们就说这棵树是优美的。根据这个定义的话,图中的树是优美的。
这个优美性的定义只对于树有效,但也可以拓展到一般的图上。
优美标号的概念最早是由 Rosa 在1967年提出的,当时他把它称作“β-valuation”,而优美标号(graceful labelling)这个名字是在1972年由 Golomb 提出的。
优美树猜想
所谓优美树猜想,其实就是如下命题:
优美树猜想(Ringel-Kötzig 猜想):所有树都是优美的。
| 顶点数目 | 树木数 |
|---|---|
| 1 | 1 |
| 2 | 1 |
| 3 | 1 |
| 4 | 2 |
| 5 | 3 |
| 6 | 6 |
| 7 | 11 |
| 8 | 23 |
| 9 | 47 |
| 10 | 106 |
| 11 | 235 |
| 12 | 551 |
| 13 | 1,301 |
| 14 | 3,159 |
| 15 | 7,741 |
| 16 | 19,320 |
| 17 | 48,629 |
| 18 | 123,867 |
| 19 | 317,955 |
| 20 | 823,065 |
| 21 | 2,144,505 |
| 22 | 5,623,756 |
| 23 | 14,828,074 |
| 24 | 39,299,897 |
| 25 | 104,636,890 |
| 26 | 279,793,450 |
| 27 | 751,065,460 |
| 28 | 2,023,443,032 |
| 29 | 5,469,566,585 |
| 30 | 14,830,871,802 |
| 31 | 40,330,829,030 |
| 32 | 109,972,410,221 |
| 33 | 300,628,862,480 |
| 34 | 823,779,631,721 |
这个猜想蕴含了 Ringel 猜想:完全图 K(2n+1) 可以被分解为 2n+1 棵含有n条边的同构的树。
直到现在,人们对这个猜想还是无从下手,但它仍然吸引了不少的数学家。Kötzig 本人有一次就曾经说过证明这个猜想的努力是一种“疾病”。
但是人们通过各种各样的方法仍然得到了一些部分的结果。现在已经证明了一些特殊的树的优美性。
一个例子就是毛毛虫树。如果一棵树去掉所有只连出一条边的顶点,剩下的部分没有分支的话,这棵树就被称为毛毛虫树。容易设计出一个算法可以有效地找出毛毛虫树的一个优美标号。所以我们说毛毛虫树是优美的。
这样的理论上的结果还有很多,但都只针对一些非常特殊的树。目前为止得到最普遍的结论就是由 P.HrnČiar 和 A.Haviar 在2001年证明的,他们证明了所有直径等于5的树都是优美的。再加上之前的结果,我们可以知道所有直径小于等于5的树都是优美的。在这里,直径的定义就是树的任意两个顶点间的最大距离,也就是说在树上任意取两个顶点,从一个顶点沿着边走到另一个顶点至少经过的边的数目。
也有数学家试图利用计算机的强大计算能力来帮助验证优美树猜想。Aldred 和 McKay 在1998年用计算机验证了所有顶点数小于等于27的树都是优美的。他们所使用的算法是爬坡搜索和禁忌搜索的结合体。
而这个项目对他们的算法进行了重大的改进,以获得更好的速度,用于验证优美树猜想。
树的数目
为什么我们需要借助空闲计算机的计算能力来做这个计算呢?
右边是一个列表,左列代表树的顶点数,右列代表含有这个数目的顶点的不同的树的数目。
可以看出,树的数目是随着顶点的数目指数增长的,大约是 O(2.99n) 。这种增长是非常快速的,所以我们需要大量的计算资源来推进优美树猜想的验证。这就是我们需要您的原因!
项目动态
- 2008/11/22 项目正式开始测试
- 2008/11/22 注册项目域名和空间,感谢 phchenjie!
- 2008/11/27 参加者 BiscuiT 返回了第一个结果,成功通过验证!
- 2008/12/10 所有测试用的工作包都已发放完毕!
- 2009/01/21 项目测试完毕,正式开始!经验证,所有含有32个顶点的树都是优美树。
- 2009/02/12 含有33个顶点的工作包已经发放完毕!开始发放含有34个顶点的工作包!
- 2009/03/07 由于技术原因,项目暂停新用户的注册以及新工作包的发放。不便之处,敬请原谅。
- 2009/04/27 所有含有33个顶点的工作包都已回收完成!经验证,所有含有33个顶点的树都是优美树。
- 2009/05/10 客户端升级,项目重新开始工作包的发放!
- 2009/06/05 含有34个顶点的工作包已经发放完毕!开始发放含有35个顶点的工作包!
- 2009/08/23 所有含有34个顶点的工作包都已回收完成!经验证,所有含有34个顶点的树都是优美树。
- 2010/02/21 所有含有35个顶点的工作包都已回收完成!经验证,所有含有35个顶点的树都是优美树。
基准测试程序及使用方法
项目提供了能估算您计算机的CPU在参与优美树验证项目时速度的程序、估算一个包所需时间的方法与一些CPU的参考速度。(详细介绍)
知道您计算机CPU的相对速度后,很容易通过简单的计算得到完成一个计算包在您的计算机上大约所需的CPU时间。在项目计算状态页面顶部,我们标注了当前正在计算的包在Core 2 Duo T7200上所需的CPU时间。只需将这个时间除以您计算机CPU的相对速度即可得出一个计算包在您的计算机上大约所需的CPU时间。
项目计算结果
目前已经完成的计算有:
- n=32:经验证所有含有32个顶点的树都是优美的(详细信息)。
- n=33:经验证所有含有33个顶点的树都是优美的(详细信息)。
- n=34:经验证所有含有34个顶点的树都是优美的(详细信息)。
- n=35:经验证所有含有35个顶点的树都是优美的(详细信息)。