优美树验证项目：修订间差异

来自中国分布式计算总站
跳转到导航 跳转到搜索
下一编辑→
Fwjmath（留言 | 贡献）
87次编辑
新页面: <big>'''优美树验证项目（Graceful Tree Verification Project）'''</big><br>验证优美树猜想<br> =='''项目简介'''== 优美树验证项目（简称GTV）是由 fwjmath 个...
 
BiscuiT（留言 | 贡献）
管理员
1,887次编辑
小无编辑摘要
第1行： 第1行：
<big>'''优美树验证项目（Graceful Tree Verification Project）'''</big><br>验证优美树猜想<br>
{{Infobox Project
=='''项目简介'''==
| name =优美树验证项目
优美树验证项目（简称GTV）是由 fwjmath 个人建立的数学类分布式计算项目.本项目旨在通过志愿分布式计算的方式对优美树猜想进行验证。优美树猜想是图论中一个重要但悬而未决的猜想，它猜想所有的树都是优美的。通过这个项目的计算，我们可以对优美树猜想进行验证，试图寻找反例，同时获得优美树的一些统计性质，帮助数学家更好的研究优美树猜想。<br>
| logo =[[Image:GTVbanner.png|230px]]
项目现正处于公开测试状态，测试用的工作包已发放完毕。
| screenshot =[[Image:GTV_screenshot.jpg|230px]]
<br><br>
| caption =优美树验证项目的运行界面
=='''加入方法'''==
| developer =[http://www.equn.com/forum/space-username-fwjmath.html fwjmath]
该项目采取电子邮件的方式传递工作包，具体流程如下：<br>
| released =2008年11月22日
1. 下载客户端并解压缩<br>
| operating system =Windows
2. 以“GTV Block Request”为题发一封电子邮件到projectgtv@gmail.com，内附你希望在网站上显示的用户名。如果有其它要求的话也可附上。<br>
| platform =独立平台
3. 主持者会回复一封带有附件的邮件。将附件中的“data.txt”下载到客户端所在的目录，运行GTVGUI.exe，然后点击“Start”按钮即可开始计算。<br>
| program size =<1MB
4. 在计算过程中，如果需要停止计算，点击“Stop”按钮即可。计算程序每隔几分钟会自动存盘，所以无须担心计算进度丢失太多。<br>
| work unit info =每个任务包里面包含了约60亿棵树，平均需要15天的计算时间，任务限期3个月。
5. 计算完毕后，客户端会自动弹出提示，此时请将客户端所在目录下的“Result.zip”作为附件回复到[email protected]，并说明你是否希望继续进行计算。<br>
| status =运行中/开发申请
6. 回到第三步，如此周而复始下去，直到你希望退出这个项目。这时请给projectgtv@gmail.com发送一封邮件说明原因.<br><br>
| genre =数学类
| optimization =无
| website =http://www.projectgtv.cn/index.html
}}
[[优美树验证项目]]（Graceful Tree Verification Project，简称GTV）是由 fwjmath 个人建立的数学类分布式计算项目.本项目旨在通过志愿分布式计算的方式对优美树猜想进行验证。优美树猜想是图论中一个重要但悬而未决的猜想，它猜想所有的树都是优美的。通过这个项目的计算，我们可以对优美树猜想进行验证，试图寻找反例，同时获得优美树的一些统计性质，帮助数学家更好的研究优美树猜想。
 
 
 
 
=='''参与方法'''==
 
该项目采取电子邮件的方式传递工作包，具体流程如下：
 
*1. 下载客户端并解压缩
 
*2. 以“GTV Block Request”为题发一封电子邮件到 projectgtv@gmail.com，内附你希望在网站上显示的用户名。如果有其它要求的话也可附上。
 
*3. 主持者会回复一封带有附件的邮件。将附件中的“data.txt”下载到客户端所在的目录，运行 GTVGUI.exe，然后点击“Start”按钮即可开始计算。
 
*4. 在计算过程中，如果需要停止计算，点击“Stop”按钮即可。计算程序每隔几分钟会自动存盘，所以无须担心计算进度丢失太多。
 
*5. 计算完毕后，客户端会自动弹出提示，此时请将客户端所在目录下的“Result.zip”作为附件回复到[email protected]，并说明你是否希望继续进行计算。
 
*6. 回到第三步，如此周而复始下去，直到你希望退出这个项目。这时请给 projectgtv@gmail.com 发送一封邮件说明原因.
 
 
=='''项目数学背景'''==
 
[[Image:GTV_T31_1.jpg|220px|right|thumb|一棵有31个顶点的树]]
===优美树的定义===
 
如图所示，这是一棵有31个顶点的树，如果您数一数的话会发现这些顶点旁边被标记了从0到30的数字，没有两个不同的顶点标记了相同的数字，而每个数字都在这棵树上出现了。这叫一个标号。
 
如果我们看边上标记的数字的话，您会发现它们恰好是这条边的两个顶点的标记数字的差。这种边上的标记就叫由顶点标号诱导出来的一个边的标号。
 
这棵树一共有30条边。如果我们仔细数一数边上的数字的话，会发现从1到30的数字都碰巧出现了，满足这种条件的标号就叫做一个优美标号（graceful labelling）。
 
一般地说，一棵拥有n个顶点的树有n-1条边，如果存在一个对顶点进行从0到n-1的不重不漏的标号，它所诱导出来的边的标号恰好不重不漏为1到n-1的话，我们就把这个顶点的标号称为一个优美标号。
 
如果一棵树能拥有至少一个优美标号的话，我们就说这棵树是优美的。根据这个定义的话，图中的树是优美的。
 
这个优美性的定义只对于树有效，但也可以拓展到一般的图上。
 
优美标号的概念最早是由Rosa在1967年提出的，当时他把它称作“β-valuation”，而优美标号（graceful labelling）这个名字是在1972年由Golomb提出的。
 
===优美树猜想===
 
所谓优美树猜想，其实就是如下命题：
优美树猜想（Ringel-Kötzig猜想）：所有树都是优美的。
 
这个猜想蕴含了Ringel猜想：完全图K(2n+1)可以被分解为2n+1棵含有n条边的同构的树。
 
直到现在，人们对这个猜想还是无从下手，但它仍然吸引了不少的数学家。Kötzig本人有一次就曾经说过证明这个猜想的努力是一种“疾病”。
 
但是人们通过各种各样的方法仍然得到了一些部分的结果。现在已经证明了一些特殊的树的优美性。
 
一个例子就是毛毛虫树。如果一棵树去掉所有只连出一条边的顶点，剩下的部分没有分支的话，这棵树就被称为毛毛虫树。容易设计出一个算法可以有效地找出毛毛虫树的一个优美标号。所以我们说毛毛虫树是优美的。
 
这样的理论上的结果还有很多，但都只针对一些非常特殊的树。目前为止得到最普遍的结论就是由P.HrnČiar和A.Haviar在2001年证明的，他们证明了所有直径等于5的树都是优美的[1]。再加上之前的结果，我们可以知道所有直径小于等于5的树都是优美的。在这里，直径的定义就是树的任意两个顶点间的最大距离，也就是说在树上任意取两个顶点，从一个顶点沿着边走到另一个顶点至少经过的边的数目。
 
也有数学家试图利用计算机的强大计算能力来帮助验证优美树猜想。Aldred和McKay在1998年用计算机验证了所有顶点数小于等于27的树都是优美的[2]。他们所使用的算法是爬坡搜索和禁忌搜索的结合体。
 
而这个项目对他们的算法进行了重大的改进，以获得更好的速度，用于验证优美树猜想。
 
===树的数目===
 
为什么我们需要借助空闲计算机的计算能力来做这个计算呢？
 
以下是一个列表，左列代表树的顶点数，右列代表含有这个数目的顶点的不同的树的数目。
 
{|border=1 align=right style="width: autoem; font-size: 100%; text-align: left; background: #f9f9f9; border: 1px #999999 solid; border-collapse: collapse;" cellpadding="2" cellspacing="0"
!顶点数目
!树木数
|-
|1
| 1
|-
|2
| 1
|-
|3
| 1
|-
|4
| 2
|-
|5
| 3
|-
|6
| 6
|-
|7
| 11
|-
|8
| 23
|-
|9
| 47
|-
|10
| 106
|-
|11
| 235
|-
|12
| 551
|-
|13
| 1,301
|-
|14
| 3,159
|-
|15
| 7,741
|-
|16
| 19,320
|-
|17
| 48,629
|-
|18
| 123,867
|-
|19
| 317,955
|-
|20
| 823,065
|-
|21
| 2,144,505
|-
|22
| 5,623,756
|-
|23
| 14,828,074
|-
|24
| 39,299,897
|-
|25
| 104,636,890
|-
|26
| 279,793,450
|-
|27
| 751,065,460
|-
|28
| 2,023,443,032
|-
|29
| 5,469,566,585
|-
|30
| 14,830,871,802
|-
|31
| 40,330,829,030
|-
|32
| 109,972,410,221
|-
|}
 
 
 
 
=='''相关链接'''==
=='''相关链接'''==
[http://www.projectgtv.cn/ 项目官方网站]<br>
*[http://www.projectgtv.cn/ 项目官方网站]
[http://www.projectgtv.cn/math_cn.html 项目数学背景]<br>
*[http://www.projectgtv.cn/math_cn.html 项目数学背景]

2009年6月8日 (一) 13:44的版本

优美树验证项目


优美树验证项目 logo

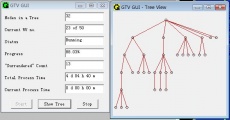优美树验证项目的运行界面
开发者 fwjmath
版本历史 2008年11月22日
运算平台 Windows
项目平台 独立平台
程序情况
任务情况 每个任务包里面包含了约60亿棵树，平均需要15天的计算时间，任务限期3个月。
项目状态 运行中/开发申请
项目类别 数学类
优化程序 无
计算特点 CPU密集：

支持0分享率：

支持GPU计算：

官方网址 优美树验证项目
{{{rss}}} [{{{rss}}} 通过 RSS 获取项目新闻]


优美树验证项目（Graceful Tree Verification Project，简称GTV）是由 fwjmath 个人建立的数学类分布式计算项目.本项目旨在通过志愿分布式计算的方式对优美树猜想进行验证。优美树猜想是图论中一个重要但悬而未决的猜想，它猜想所有的树都是优美的。通过这个项目的计算，我们可以对优美树猜想进行验证，试图寻找反例，同时获得优美树的一些统计性质，帮助数学家更好的研究优美树猜想。



参与方法

该项目采取电子邮件的方式传递工作包，具体流程如下：

  • 1. 下载客户端并解压缩
  • 2. 以“GTV Block Request”为题发一封电子邮件到 [email protected]，内附你希望在网站上显示的用户名。如果有其它要求的话也可附上。
  • 3. 主持者会回复一封带有附件的邮件。将附件中的“data.txt”下载到客户端所在的目录，运行 GTVGUI.exe，然后点击“Start”按钮即可开始计算。
  • 4. 在计算过程中，如果需要停止计算，点击“Stop”按钮即可。计算程序每隔几分钟会自动存盘，所以无须担心计算进度丢失太多。
  • 5. 计算完毕后，客户端会自动弹出提示，此时请将客户端所在目录下的“Result.zip”作为附件回复到[email protected]，并说明你是否希望继续进行计算。
  • 6. 回到第三步，如此周而复始下去，直到你希望退出这个项目。这时请给 [email protected] 发送一封邮件说明原因.


项目数学背景

一棵有31个顶点的树

优美树的定义

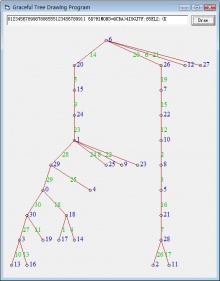
如图所示，这是一棵有31个顶点的树，如果您数一数的话会发现这些顶点旁边被标记了从0到30的数字，没有两个不同的顶点标记了相同的数字，而每个数字都在这棵树上出现了。这叫一个标号。

如果我们看边上标记的数字的话，您会发现它们恰好是这条边的两个顶点的标记数字的差。这种边上的标记就叫由顶点标号诱导出来的一个边的标号。

这棵树一共有30条边。如果我们仔细数一数边上的数字的话，会发现从1到30的数字都碰巧出现了，满足这种条件的标号就叫做一个优美标号（graceful labelling）。

一般地说，一棵拥有n个顶点的树有n-1条边，如果存在一个对顶点进行从0到n-1的不重不漏的标号，它所诱导出来的边的标号恰好不重不漏为1到n-1的话，我们就把这个顶点的标号称为一个优美标号。

如果一棵树能拥有至少一个优美标号的话，我们就说这棵树是优美的。根据这个定义的话，图中的树是优美的。

这个优美性的定义只对于树有效，但也可以拓展到一般的图上。

优美标号的概念最早是由Rosa在1967年提出的，当时他把它称作“β-valuation”，而优美标号（graceful labelling）这个名字是在1972年由Golomb提出的。

优美树猜想

所谓优美树猜想，其实就是如下命题： 

优美树猜想（Ringel-Kötzig猜想）：所有树都是优美的。

这个猜想蕴含了Ringel猜想：完全图K(2n+1)可以被分解为2n+1棵含有n条边的同构的树。

直到现在，人们对这个猜想还是无从下手，但它仍然吸引了不少的数学家。Kötzig本人有一次就曾经说过证明这个猜想的努力是一种“疾病”。

但是人们通过各种各样的方法仍然得到了一些部分的结果。现在已经证明了一些特殊的树的优美性。

一个例子就是毛毛虫树。如果一棵树去掉所有只连出一条边的顶点，剩下的部分没有分支的话，这棵树就被称为毛毛虫树。容易设计出一个算法可以有效地找出毛毛虫树的一个优美标号。所以我们说毛毛虫树是优美的。

这样的理论上的结果还有很多，但都只针对一些非常特殊的树。目前为止得到最普遍的结论就是由P.HrnČiar和A.Haviar在2001年证明的，他们证明了所有直径等于5的树都是优美的[1]。再加上之前的结果，我们可以知道所有直径小于等于5的树都是优美的。在这里，直径的定义就是树的任意两个顶点间的最大距离，也就是说在树上任意取两个顶点，从一个顶点沿着边走到另一个顶点至少经过的边的数目。

也有数学家试图利用计算机的强大计算能力来帮助验证优美树猜想。Aldred和McKay在1998年用计算机验证了所有顶点数小于等于27的树都是优美的[2]。他们所使用的算法是爬坡搜索和禁忌搜索的结合体。

而这个项目对他们的算法进行了重大的改进，以获得更好的速度，用于验证优美树猜想。

树的数目

为什么我们需要借助空闲计算机的计算能力来做这个计算呢？

以下是一个列表，左列代表树的顶点数，右列代表含有这个数目的顶点的不同的树的数目。

顶点数目 树木数
1 1
2 1
3 1
4 2
5 3
6 6
7 11
8 23
9 47
10 106
11 235
12 551
13 1,301
14 3,159
15 7,741
16 19,320
17 48,629
18 123,867
19 317,955
20 823,065
21 2,144,505
22 5,623,756
23 14,828,074
24 39,299,897
25 104,636,890
26 279,793,450
27 751,065,460
28 2,023,443,032
29 5,469,566,585
30 14,830,871,802
31 40,330,829,030
32 109,972,410,221



相关链接

检索自“https://equn.com/w/index.php?title=优美树验证项目&oldid=2513”